Olá, pessoal, tudo beleza? Nesta aula, vamos falar sobre Gravitação, mais especificamente a energia potencial gravitacional. Já adianto que esse não é um dos temas que mais caem nas provas, mas dominá-lo pode ser um importante diferencial na nota final.
Lápis e caderno na mão, acompanhe e bons estudos!
Energia Potencial Gravitacional
A primeira coisa que temos que destacar é que essa matéria se aplica a corpos em um ambiente com gravidade variável, ou seja, não se aplica a corpos próximos da Terra, em que consideramos que a gravidade (g) é constante.
Vamos lembrar: se g for constante (próximo ao planeta), calcularemos a Energia Potencial Gravitacional por: Epg = m . g . h.
No entanto, se a gravidade variar, isto é, quando a distância para o planeta variar, precisaremos de outra equação:
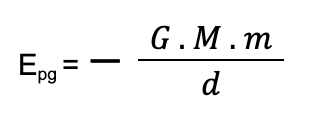
- G: Constante de Gravitação Universal (valor aproximado de 6,7 . 10-11 N.m²/kg²).
- M e m: massas dos corpos do sistema.
- d: distância do centro de um astro ao centro do outro corpo (medida em metros).
Veja a imagem:
Um detalhe muito importante ao estudarmos essa matéria é que o referencial adotado é no infinito. Isso significa que, no infinito, a Energia Potencial Gravitacional do sistema é nula (Epg = 0).
Energia Mecânica
Geralmente, quando temos que calcular a Energia Mecânica de um sistema de corpos, somamos da Energia Cinética com a Energia Potencial:
Em = Ec + Ep.
Quando falamos de Energia Potencial Gravitacional, a ideia é a mesma. Porém, embora o cálculo da Energia Cinética seja o mesmo, a Energia Potencial precisará ser calculada com a fórmula que vimos acima.
De maneira geral, os exercícios sobre essa matéria se basearão em sistemas conservativos, em que não há atrito (por ser no espaço) e, assim, a Energia Mecânica fica constante:
Em final = Em inicial
Entenda que não é a Energia Cinética nem a Potencial que ficam constantes (Em = Ec + Ep), mas a soma das energias
Ec final + Ep final = Ec inicial + Ep inicial
Então, em questões em que a Energia Cinética aumenta, isso implica que, necessariamente, a Energia Potencial Gravitacional diminui. Isso vai acontecer quando tivermos o chamado movimento espontâneo.
O contrário de um movimento espontâneo é o chamado movimento forçado. Então, se a Energia Cinética diminuir, a Energia Potencial Gravitacional vai aumentar.
Energia nas órbitas elípticas
Veja a imagem de um corpo em trajetória elíptica ao redor do sol no sentido anti-horário:
Sabemos que a força gravitacional exercida pelo Sol no corpo possui uma componente tangencial a favor do movimento (quando os corpos se aproximam), que faz com que a velocidade do corpo aumente (e a Energia Cinética também). Isso se chama de movimento acelerado.
Já quando o corpo se afasta, o inverso acontece. Há um movimento retardado, ou seja, ele perde velocidade. Aqui, é importante lembrar que, quando se perde velocidade, perde-se também Energia Cinética.
Dessa forma, a velocidade máxima de um corpo em órbita elíptica será alcançada num ponto chamado de Periélio. Já o ponto de menor velocidade chama-se Afélio.
Lembre-se de que estamos em um sistema conservativo (Em = Ec + Ep). Como a Energia Mecânica é constante, toda vez que a Energia Cinética for máxima, a Energia Potencial será mínima. E vice-versa.
Resumindo:
Velocidade de escape
É preciso ter muito cuidado com duas velocidades que costumam aparecer nessa matéria. Uma delas é a velocidade cósmica primeira, que é a velocidade com que um corpo deve ser lançado, de forma rasante ao astro, para que ele permaneça em órbita circular, “preso” na gravidade do planeta.
Para calcular essa velocidade, temos que considerar que a força gravitacional atua como variante centrípeta. Assumindo que a Resultante Centrípeta é igual ao Peso (Rc = P), temos que:
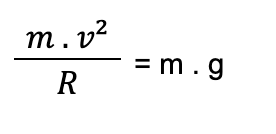
Então, chegamos a que a velocidade para que o corpo ficasse em órbita seria calculada pela raiz quadrada do raio da órbita multiplicado pelo gravidade do planeta 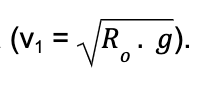
Mas atenção: esse é o cálculo para a velocidade para manter um corpo em órbita circular. Isso posto, poderíamos ter calculado isso de outra forma:
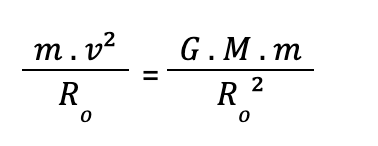
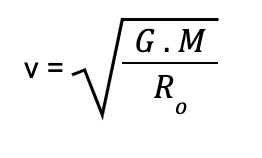
Note que ambas as fórmulas calculam a mesma coisa. Porém, na primeira equação, temos que conhecer o campo gravitacional do local. Por isso, só utilizamos a primeira quando a órbita é rasante ao planeta. Caso o corpo esteja longe, é melhor utilizarmos a segunda fórmula.
Nesse sentido, temos que falar da velocidade de escape (Ve). Trata-se da velocidade necessária para que o corpo escape da ação gravitacional do planeta, isto é, para que ele não fique preso na órbita. Queremos, portanto, saber a velocidade mínima necessária para que esse corpo escape e se perca no infinito, quando ele para.
Em final = Em inicial
Ecf + Epf = Eci + Epi
Note que a Energia Cinética final será nula, pois o corpo chegará ao infinito parado. Da mesma forma, a Energia Potencial final também é nula, uma vez que o referencial está no infinito. Ou seja:
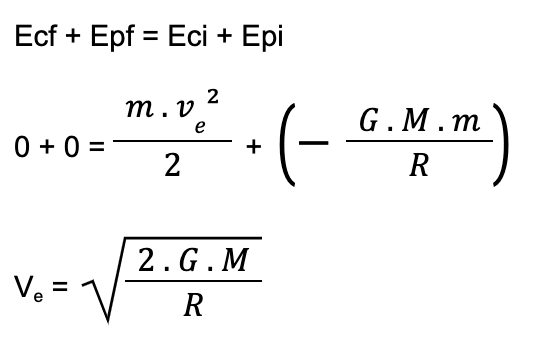
Lembrando que:
- R se trata do raio do planeta de onde o corpo foi lançado, e não o raio da órbita.
- M se refere à massa do planeta de onde o corpo foi lançado.
Exemplo de exercício de Energia Potencial Gravitacional
a) Determine a velocidade para manter um corpo em órbita circular rasante ao redor do Planeta Terra.
b) Determine a velocidade de escape para um corpo lançado tangencialmente a partir da superfície do Planeta Terra.
Dados: g da Terra = 10 N/kg; M da terra = 6.1024 kg; Raio da Terra = 6370 km; Constante de Gravitação Universal = 6,67 . 10-11 N.m²/kg².
a) Quando um corpo fica em órbita circular ao redor da Terra, é a força peso (P) que o mantém na órbita. Então devemos igualar a Resultante Centrípeta ao Peso.
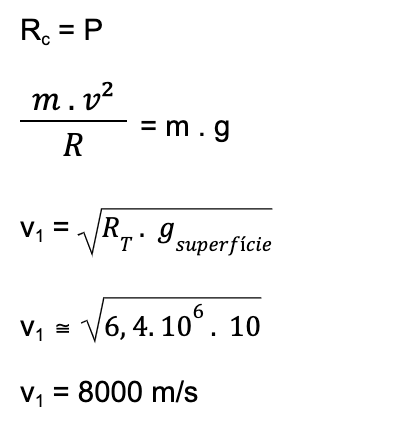
b) Vamos usar Energia Mecânica:
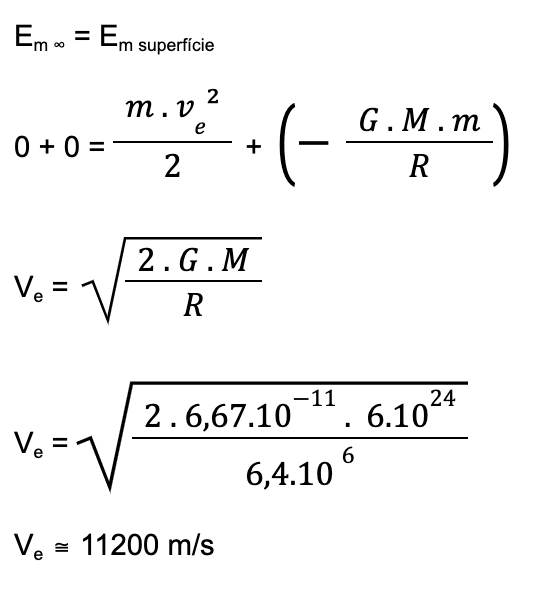
–
Espero que você tenha entendido um pouco melhor sobre Energia Potencial Gravitacional e os cálculos que podemos fazer. E se quiser ajuda para melhorar seu nível de Física em outras matérias, entre em contato comigo e escolha o curso de Física mais adequado para você!
SAIBA MAIS
👉 Exercícios de Energia Mecânica
👉 Como estudar sobre Eletricidade para vestibulares paulistas
👉 Questões de Cinemática para o ENEM
Me acompanhe nas redes sociais: curta a minha página no Facebook, me siga no Instagram, se inscreva no Youtube e participe do meu canal oficial no Telegram.

