Leis de Newton – Exercícios de Blocos e Atrito
Neste post, vamos resolver juntos 3 exercícios sobre a aplicação das Leis de Newton – Blocos e Atrito. São questões básicas, mas úteis para entendermos como podemos lidar com problemas que envolvem blocos, com e sem atrito.
Portanto, lápis e borracha na mão e vamos lá!
Questão 1
(Fuvest) A figura mostra dois blocos A e B empurrados por uma força horizontal, constante, de intensidade F = 6,0 N, em um plano horizontal sem atrito. O bloco A tem massa de 2,0 kg e o bloco B tem massa de 1,0 kg.
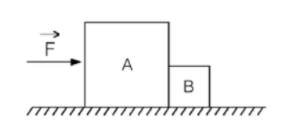
a) Qual o módulo da aceleração do conjunto?
Para resolvermos essa questão, podemos separar o corpo A do corpo B. Mas isso não é necessário. Podemos considerar o conjunto como um todo e seria como se uma força só fosse aplicada ao conjunto. Portanto:
FR = msistema . a
6 = (2 + 1) . a
a = 2 m/s²
b) Qual a intensidade da força que A exerce em B?
Para sabermos a força trocada entre A e B, podemos tanto isolar um quanto o outro. Vamos isolar o B: repare que, verticalmente sobre esse corpo, existe uma força normal que, neste caso, é anulada pelo peso do corpo. Além disso, incide também a força que A exerce sobre B (horizontal, para a direita).
Cuidado para respeitar a aceleração do sistema, a mesma que encontramos no primeiro item da questão. Como ele está acelerando para direita e a força que A exerce sobre B é a única força horizontal, então ficamos com:
FR = mB . a
FAB = 1 . 2
FAB = 2 N
Para confirmar, vamos isolar o corpo A desta vez: sobre ele, é exercida F = 6 N, conforme dado no enunciado, e a força de reação a que A exerce sobre B que é o oposto, ou seja, a força que B exerce sobre A.
Como aceleração está para a direita, quem está ajudando o sistema a acelera é a força de 6 N. Portanto:
FR = mA . a
6 – FBA = 2. 2
FBA = 2 N
Questão 2
(Vunesp -SP modificada) Dois blocos A e B, de massas 2,0 kg e 6,0 kg, respectivamente, e ligados por um fio, estão em repouso sobre um plano horizontal. Quando puxado para a direita pela força F mostrada na figura, o conjunto adquire aceleração de 3,0 m/s2. Determine
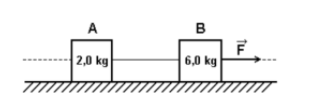
a) a intensidade da força F.
Como não há atrito, podemos assumir que todo o conjunto tem uma mesma aceleração e está sendo puxado por uma força só. Portanto:
FR = msist . a
F = (2 + 6) . 3
F = 24 N
b) a intensidade da tração no fio que une os corpos A e B.
Note que a tração em ambas as pontas do fio tem o mesmo valor, uma vez que o fio é ideal. Assim, podemos escolher arbitrariamente qual dos corpos desejamos isolar.
Escolhi isolar o A: sobre ele, há a tração (T) para a direita, a normal e o peso que se anulam verticalmente e a aceleração que também é para a direita, ou seja, no mesmo sentido da força.
Assim:
FR = mA . a
T = 2 . 3
T = 6 N
Questão 3
No esquema a seguir, não existem forças de atrito. Os blocos A e B têm massas iguais a 1,0 kg e o bloco C tem massa 3 kg e estão sobre um plano horizontal.
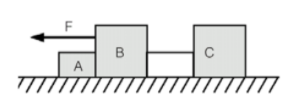
A força F é horizontal, constante e de intensidade 15 N. Determine
a) a aceleração do conjunto de corpos
Novamente a mesma idéia: podemos agrupar todos os blocos em um único conjunto, neste caso com 5 kg. Então:
FR = msist . a
15 = 5 . a
a = 3 m/s²
b) a intensidade da força tensora no fio.
Para calcularmos a tração (T) no fio, podemos isolar tanto o bloco B quanto o C, pois a força tensora é a mesma nas duas pontas. Nesse caso, fica mais fácil isolar o bloco C, pois só há uma força que atua nele, que é a tração do fio (peso e normal se anulam verticalmente). E atenção, porque a força F dada na figura só atua sobre a força B!
FR = mC . a
T = 3 . 3
T = 9 N
c) a intensidade da força que B exerce em A.
A força que A exerce em B tem a mesma força que B exerce em A. Então, podemos isolar qualquer um dos corpos. Porém, repare que isolar o B seria mais difícil, pois há muitas forças exercidas sobre ele.
Por isso, vamos isolar o A: peso e normal se anulam. Assim, no corpo A a única força que atua é justamente a que o corpo B exerce sobre ele. Nessa questão, todo o conjunto acelera para a esquerda.
FR = mA . a
FBA = 1 . 3
FBA = 3 N
–
Para aprofundar ainda mais seus estudos, convido você a assistir à videoaula Exercícios de Blocos e Atrito – Básico, em que resolvo 12 questões (incluindo essas três) sobre blocos e atrito.
E se quiser ajuda para melhorar seu nível de Física em outras matérias, entre em contato comigo e escolha o curso de Física mais adequado para você!

SAIBA MAIS
✅ Questões de Cinemática resolvidas em vídeo
✅ Conceitos básicos de Cinemática: Equação do espaço em função do tempo
✅ Tudo sobre Cinemática: Revisão das principais questões dos vestibulares Paulista
Me acompanhe nas redes sociais: curta a minha página no Facebook, me siga no Instagram, se inscreva no Youtube e participe do meu canal oficial no Telegram.

