Hoje, vamos fazer alguns exercícios sobre a Leis de Kirchhoff, mas antes, iremos revisar alguns conceitos e fórmulas importantes. Acompanhe!
O que são as Leis de Kirchhoff
As leis recebem esse nome pois foram criadas pelo físico Gustav Robert Kirchhoff. Elas se baseiam no princípio da conservação de carga elétrica e são utilizadas para analisar circuitos elétricos complexos (que não podem ser reduzidos a circuitos simples) e identificar as intensidades das correntes.
Para entendermos bem as Leis de Kirchhoff, precisamos entender bem alguns conceitos fundamentais. Três deles são:
- Nós: encontro de três ou mais fios.
- Malha: percursos fechados que se iniciam em um nó e voltam ao mesmo ponto.
- Ramo: trechos de circuitos – ou pedaço de fio – entre dois nós.
As Leis de Kirchhoff
Kirchhoff elaborou duas leis. São elas:
Primeira Lei de Kirchhoff ou Lei dos Nós
Afirma que a soma das correntes que chegam a um nó é igual à soma das correntes que saem do nó, independentemente do fenômeno.
Σi entra = Σi sai
Segunda Lei de Kirchhoff ou Lei das Malhas
Afirma que, percorrendo-se uma malha em um determinado sentido, partindo-se e chegando-se ao mesmo ponto, a soma algébrica das tensões elétricas (ddp ou diferenças de potencial) é igual a zero.
ΣUAA = 0
Cálculos
Quando falamos de Leis de Kirchhoff, existem alguns cálculos que podem ser cobrados pelos vestibulares. O primeiro deles diz respeito à diferença de potencial elétrico (ddp) dos resistores.
A fórmula é a seguinte: U = R.i
- U = potencial elétrico (V)
- R = resistência elétrica (Ω)
- i = corrente elétrica (A)
A tensão poderá ser positiva ou negativa, dependendo do sentido que definimos para a corrente percorrer pelo circuito. Assim:
- Quando o percurso se dá a favor da corrente, teremos: U = + R.i
- Quando o percurso se dá contra a corrente, teremos: U = – R.i
Já quando vamos calcular a diferença de potencial elétrico em terminais, é importante lembrar que, nos geradores (fem), a corrente entra pelo terminal negativo e sai pelo terminal positivo. Por sua vez, nos receptores (fcem), a corrente elétrica entra pelo terminal positivo e sai pelo terminal negativo.
Com isso mente, quando vamos calcular a diferença de ddp em terminal fem ou fcem, o sinal de entrada do percurso é o que determina o sinal ddp que você está lendo:
- Quando o percurso entra pelo terminal positivo, teremos: UAB = + E
- Quando o percurso entra pelo terminal negativo: UBA = – E
Exemplos de aplicações das Leis de Kirchhoff
Exemplo com apenas uma malha
Observe a malha abaixo e calcule a ddp entre os pontos A e D:
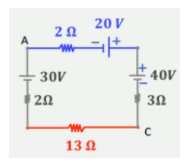
Perceba que, de acordo com a Lei das Malhas, quando saímos de um ponto e retornamos a esse mesmo ponto, a soma deve ser igual a zero.
Aqui, é importante percebermos que o sentido da corrente não foi estipulado. Nesse caso, nós devemos arbitrar um sentido qualquer. Para este exemplo, vamos considerar que a corrente possui sentido anti-horário. Dessa forma, partindo do ponto A, temos:
- +30 + 2i + 13 + 3i – 40 + 20 + 2i = 0
Para prosseguir com o cálculo, devemos somar os termos semelhantes. Assim:
- 20i + 10 = 0
- 20i = -10
- i = – 0.5 A
Atenção: perceba que a corrente deu negativo, o que não é possível. Isso não significa que nossos cálculos estão errados, mas somente que arbitramos o sentido errado à corrente. Portanto, o sentido correto é, na verdade, horário, resultando em: i = 0,5 A
Exemplo com múltiplas malhas
Repare que o nosso exemplo acima conta com apenas uma malha. Assim, quando o circuito contar com diversas malhas, devemos seguir os seguintes passos:
- 1º passo: escolher arbitrariamente os sentidos das correntes em cada ramo.
- 2º passo: aplicar a Lei dos Nós (Σi entra = Σi sai). Esta é nossa primeira equação que utilizaremos para resolver a questão.
- 3º passo: aplicar a Lei das Malhas. Para isso, em primeiro lugar, é necessário escolher um sentido de percurso. Em seguida, é necessário partir de um ponto e retornar ao mesmo ponto somando as ddps (UAA = 0). Esta é nossa segunda equação.
- 4º passo: aplicar a 2ª lei de Kirchhoff na próxima malha. Esta é nossa terceira equação.
- 5º passo: resolver o sistema de equações.
Atenção: após calcular as correntes, se algum valor der negativo, isso significa que o sentido escolhido para a corrente está errado. Lembre-se de que o valor da corrente é o módulo do valor encontrado.
Explicações feitas, veja o sistema abaixo:
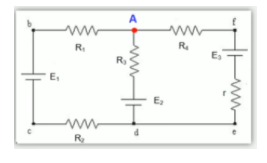
Seguindo o passo a passo acima, devemos escolher um sentido para nossas correntes em cada um dos ramos. Vamos fazer isso de maneira arbitrária, no chute:
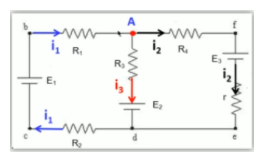
Continuemos no passo a passo, aplicamos a Lei dos Nós para termos nossa primeira equação:
- Nó A: i1 = i2 + i3
Em seguida, devemos resolver cada uma das malhas. Vamos começar pela malha da esquerda da imagem, partindo do ponto A e retornando ao mesmo ponto A. Teremos nossa segunda equação:
- R3.i3 + E2 + R2.i1 – E1 + R1.i1 = 0
Agora, vamos elaborar nossa terceira equação. Para isso, vamos resolver a malha da direita da imagem, novamente partindo do ponto A e retornando a ele:
- R4.i2 + E3 + r.i2 – E2 – R3.i3 = 0
Exercícios de Leis de Kirchhoff
Questão 1
(Udesc) De acordo com a figura, os valores das correntes elétricas i1, i2 e i₃ são, respectivamente, iguais a:

a) 2,0 A, 3,0 A, 5,0 A
b) -2,0 A, 3,0 A, 5,0 A
c) 3,0 A, 2,0 A, 5,0 A
d) 5,0 A, 3,0 A, 8,0 A
e) 2,0 A, -3,0 A, -5,0 A
Resposta: A
Questão 2
(ITA) Considere o circuito elétrico mostrado na figura formado por quatro resistores de mesma resistência, R = 10 Ω, e dois geradores ideais cujas respectivas forças eletromotrizes são ε1 = 30 V e ε2 = 10 V. Pode-se afirmar que as correntes i1, i2, i3 e i4 nos trechos indicados na figura, em ampères, são respectivamente de

a) 2, 2/3, 5/3 e 4
b) 7/3, 2/3, 5/3 e 4
c) 4, 4/3, 2/3 e 2
d) 2, 4/3, 7/3 e 5/3
e) 2, 2/3, 4/3 e 4
Resposta: B
Questão 3
(Espcex – Aman) O desenho abaixo representa um circuito elétrico composto por resistores ôhmicos, um gerador ideal e um receptor ideal.
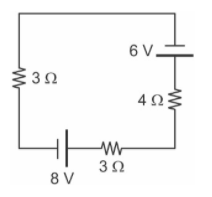
A potência elétrica dissipada no resistor de 4 Ω do circuito é:
a) 0,16 W
b) 0,20 W
c) 0,40 W
d) 0,72 W
e) 0,80 W
Resposta: A
Questão 4
(Unesp) Três resistores, P, Q e S, cujas resistências valem 10, 20 e 20 ohms, respectivamente, estão ligados ao ponto A de um circuito. As correntes que passam por P e Q são 1,00 A e 0,50 A, como mostra a figura adiante.
Determine as diferenças de potencial:
a) entre A e C;
b) entre B e C.
Resposta: A) 30 V; B) 40 V
Ainda com dúvidas sobre Leis de Kirchhoff?
Aperte o play e assista a videoaula completa sobre o assunto!
Espero que você tenha entendido um pouco melhor. E se quiser ajuda para melhorar seu nível de Física em outras matérias, entre em contato comigo e escolha o curso de Física mais adequado para você!

SAIBA MAIS
✅ Receptores elétricos
✅ Associação de geradores
✅ Tudo sobre Cinemática
Me acompanhe nas redes sociais: curta a minha página no Facebook, me siga no Instagram, se inscreva no Youtube e participe do meu canal oficial no Telegram.

