Fala, pessoal, tranquilo? Na aula de hoje, vamos estudar o Princípio de Pascal ou Prensa Hidráulica, um dos assuntos da matéria de Hidrostática. Acompanhe!
Princípio de Pascal (Prensa Hidráulica)
O Princípio de Pascal é o que rege algumas máquinas que permitem ganhar uma vantagem mecânica para exercer uma força. Veja a figura:
Trata-se de um sistema de fluido que possui dois êmbolos. Para manter o carro da figura parado, exerce-se uma força (F1) do outro lado sobre um êmbolo que possui uma área (A1), ou seja, estamos fazendo uma pressão.
Pascal descobriu que, quando isso acontece, a pressão exercida em um ponto se transmite para todos os outros pontos do recipiente do mesmo líquido. Então, ao exercer F1, aumenta-se a pressão do sistema, gerando uma nova força (F2) no êmbolo de área maior (A2).
Quando falamos dos cálculos envolvendo o Princípio de Pascal, temos que considerar, como vimos, que a variação de pressão produzida num ponto do líquido é transferida aos outros pontos do mesmo líquido, isto é:
Δp1 = Δp2
Lembre-se de que a pressão se dá pela razão da força (F) pela área (A), medida em N/m²:

Nessa fórmula, repare que a força é diretamente proporcional à área. Isso significa que o lado cujo êmbolo tem maior área é o lado onde há mais força. Com isso, a Prensa Hidráulica consegue aumentar a força realizada, transformando uma força pequena em uma área pequena em uma força grande em uma área grande.
Exemplo: se A2 = 10 . A1, então F2 = 10 . F1
Importante notar que a Prensa Hidráulica possui um problema. O deslocamento de um êmbolo não será o mesmo gerado no outro. Para entender isso, precisamos lembrar de trabalho (W):
W = F . d
Desprezando o atrito, temos que o trabalho nos dois lados da prensa é o mesmo. Portanto, no lado onde houver mais força, haverá menos deslocamento. Assim, quando dizemos que A2 = 10 . A1, então F2 = 10 . F1, o mesmo não vale para o deslocamento.
Nesse caso, a altura que o êmbolo 2 sobe (H2) será um décimo da altura que o êmbolo 1 desceu (H1):
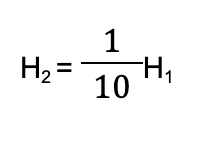
Exemplo exercícios Prensa Hidráulica
(FGV) O macaco hidráulico consta de dois êmbolos: um estreito, que comprime o óleo, e outro largo, que suspende a carga. Um sistema de válvulas permite que uma nova quantidade de óleo entre no mecanismo sem que haja retorno do óleo já comprimido. Para multiplicar a força empregada, uma alavanca é conectada ao corpo do macaco.
Tendo perdido a alavanca do macaco, um caminhoneiro de massa 80 kg, usando seu peso para pressionar o êmbolo pequeno com o pé, considerando que o sistema de válvulas não interfira significativamente sobre a pressurização do óleo, poderá suspender uma carga máxima em kg?
Dados: diâmetro do êmbolo menor = 1,0 cm; diâmetro do êmbolo maior = 6,0 cm; aceleração da gravidade = 10 m/s².
a) 2.880.
b) 2.960.
c) 2.990
d) 3.320.
e) 3.510.
RESOLUÇÃO:
Note, então, que o caminhoneiro vai exercer uma força (F1) em uma área pequena (A1) para gerar uma força (F2) na área maior (A2).
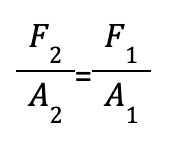
Vamos considerar a força com o mesmo valor do peso. Antes de seguir, porém, precisamos descobrir a área dos êmbolos.
Veja que nos foram dados os diâmetros dos êmbolos, o que nos leva a que r2 = 6 . r1. Então:
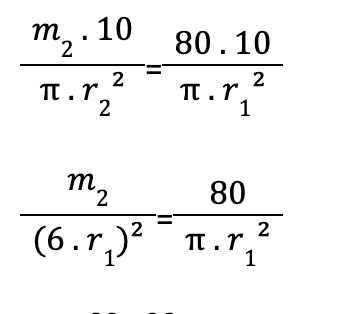
m2 = 80 . 36
m2 = 2880 kg
RESPOSTA: A
–
Espero que você tenha entendido um pouco melhor sobre o Princípio de Pascal, Prensa Hidráulica e os cálculos que podemos fazer. E se quiser ajuda para melhorar seu nível de Física em outras matérias, entre em contato comigo e escolha o curso de Física mais adequado para você!
SAIBA MAIS
👉 O que são instrumentos ópticos
👉 Exercícios sobre Análise Dimensional
👉 Os melhores filmes e séries para quem gosta de Física
Me acompanhe nas redes sociais: curta a minha página no Facebook, me siga no Instagram, se inscreva no Youtube e participe do meu canal oficial no Telegram.

