Exercícios sobre Vetores
Questão 1
Um automóvel se desloca 6 km para norte e, em seguida, 8 km para o leste. Determine a intensidade do vetor deslocamento.
Vamos chamar o deslocamento para o norte de d1 e o deslocamento para o leste de d2. Veja:
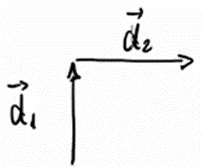
Pela regra do polígono de soma vetorial, basta ligarmos os dois deslocamentos (início de um com o final de outro) para formarmos, neste caso, um triângulo retângulo. A este novo vetor daremos o nome de deslocamento total (dT). Observe:
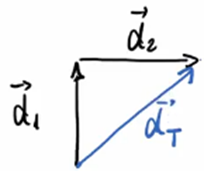
Importante: dT = d1 + d2. No entanto, não devemos substituir esses elementos por números. Como nesta questão a figura formada foi um triângulo retângulo, então devemos utilizar Pitágoras:Ç
dT² = 6² + 8²
dT = 10 km
Questão 2
Uma pessoa caminha em uma planície realizando três movimentos retilíneos: primeiro percorre 10 km de sul para norte; em seguida, percorre 6 km de oeste para leste; finalmente, caminha mais dois quilômetros de norte para sul.
a) Desenhe os vetores deslocamento de cada trecho, assim como o vetor deslocamento total, d
De novo: o primeiro deslocamento, de 10 km para norte, chamaremos de d1 . O segundo, para leste, daremos o nome de d2 . Por fim, o último, para o sul, será nosso d3. Veja:
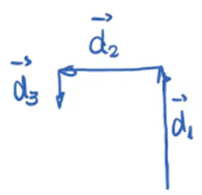
Para encontrar o deslocamento total pedido pela questão, mais uma vez devemos ligar o início do primeiro ao final do último trecho:
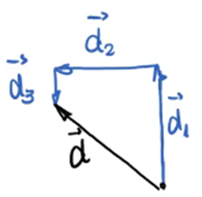
b) Calcule o módulo de d.
Lembre-se de que o deslocamento final é igual à soma vetorial dos outros três deslocamentos: d = d1 + d2 + d3
Como não podemos colocar números nessa equação de vetores, para calcular o módulo, podemos colocar na figura quanto vale cada lado da figura formada pelos deslocamentos:
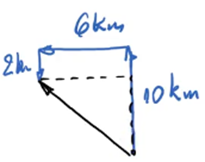
Note que, para encontrarmos o deslocamento total, podemos formar um triângulo em que o lado que queremos descobrir desempenha o papel da hipotenusa. Portanto, o deslocamento pedido pela questão, tem um cateto que vale 6 e outro que vale 8 (repare na figura: 10 – 2).
Novamente lançando mão de Pitágoras, temos:
d² = 6² + 8²
d = 10 km
Questão 3
(PUCCAMP 98) Num bairro, onde todos os quarteirões são quadrados e as ruas paralelas distam 100m uma da outra, um transeunte faz o percurso de P a Q pela trajetória representada no esquema a seguir.
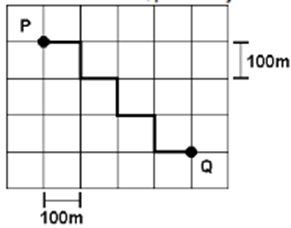
O deslocamento vetorial desse transeunte tem módulo, em metros, igual a
a) 300
b) 350
c) 400
d) 500
e) 700
Para calcularmos o deslocamento vetorial, temos que desenhar o vetor que parte do ponto P ao Q. Portanto:
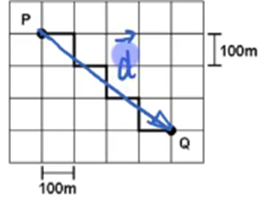
Repare que, para calcular o módulo, novamente vamos utilizar a figura formada. Afinal, temos o valor dos catetos que serão formados:
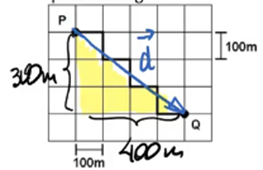
Assim: d² = 300² + 400²
d = 500 m
RESPOSTA: D
Questão 4
Um pássaro voa em linha reta do ponto A, no solo, ao ponto B, em uma montanha, que dista 800 m do ponto A ao longo da horizontal. O ponto B se encontra também a uma altura de 600 m em relação ao solo.Dado que a velocidade do pássaro é de 10 m/s, determine o intervalo de tempo que ele leva para percorrer a distância de A a B. (considere g = 10 m/s2).
Note que o ponto A está na horizontal e o ponto B está na vertical:
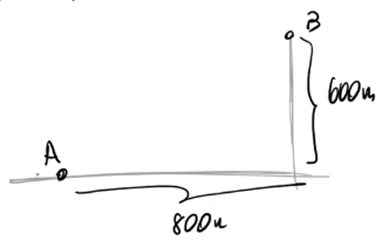
Você já deve ter percebido que o deslocamento entre A e B vai formar um triângulo retângulo. Portanto:
d² = 600² + 800²
d = 1000 m
Agora, como a questão pede o tempo, vamos usar a fórmula da velocidade:
v=Δs/Δt
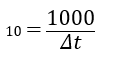
Δt = 100 s
Questão 5
Desenhe o vetor :
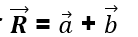
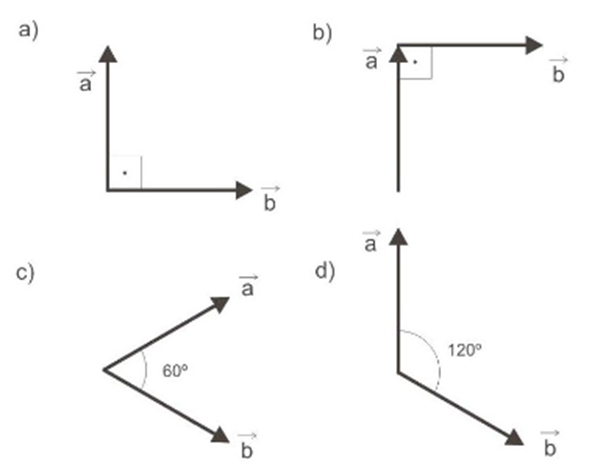
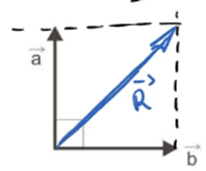
a) Veja que, quando os vetores estão desenhados com a mesma origem, podemos usar a regra do paralelogramo:
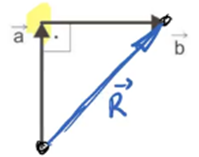
b) Quando temos um vetor saindo da origem de outro, devemos utilizar a regra do polígono, unindo a origem de um com o final de outro:
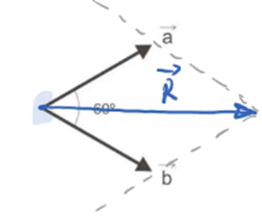
c) Novamente os vetores estão com a mesma origem. Então, vamos traçar as paralelas:
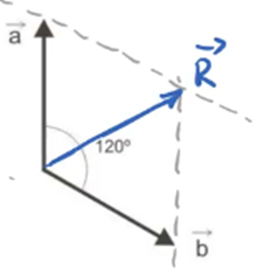
d) Mesma solução:
Questão 6
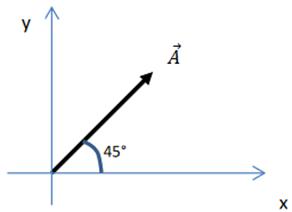
O vetor A a seguir tem módulo 40 unidades. Determine suas componentes horizontal e vertical.
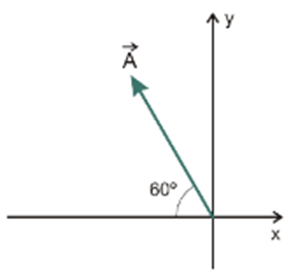
Nesta questão, devemos decompor os vetores. Para isso, devemos traçar em A uma paralela ao eixo y. Isso nos dará o vetor Ax.
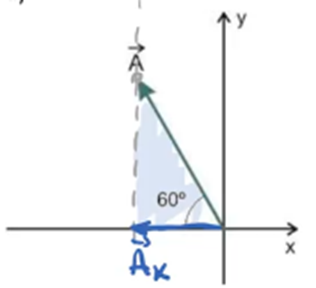
Note que formaremos um triângulo, do qual teremos que utilizar o cosseno do ângulo de 60º:
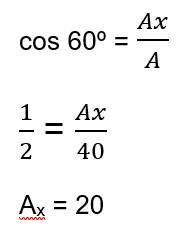
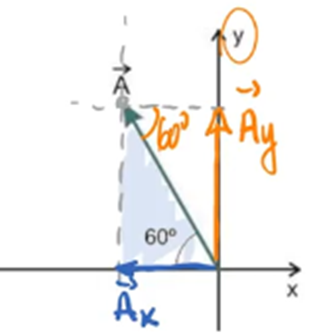
Para encontrar o outro componente, precisamos traçar em A uma paralela no eixo x, que nos dará Ay. Novamente, formaremos um triângulo. E repara que, pela conformação da figura, o ângulo será o mesmo, só que dessa vez será o seno:
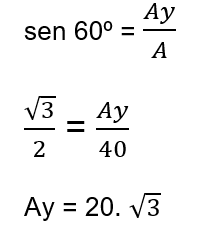
Faremos a mesma coisa. Comecemos traçando uma paralela ao eixo y para encontramos o vetor Ax.

Agora note que, quando o ângulo é 45º, o vetor A corta um ângulo de 90º exatamente na metade. Portanto, a componente Ay tem o mesmo tamanho que Ax:
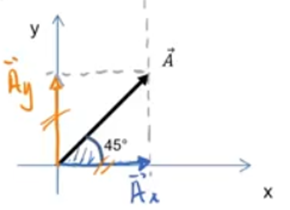
Se você quiser fazer as contas mesmo assim:

Para aprender um pouco mais sobre vetores, assista minha videoaula abaixo:
Aula 1
Aula 2
E se quiser ajuda para melhorar seu nível de Física em outras matérias, entre em contato comigo e escolha o curso de Física mais adequado para você!

SAIBA MAIS
👉 Projeção de um vetor em dois eixos
👉 Como estudar Eletricidade para vestibulares paulista
👉 Tudo sobre a Terceira Lei de Newton
Me acompanhe nas redes sociais: curta a minha página no Facebook, me siga no Instagram, se inscreva no Youtube e participe do meu canal oficial no Telegram.



