Nesta aula, vamos fazer uma revisão sobre polias e roldanas na prática, isto é, vamos resolver alguns exercícios para rever as principais fórmulas e conceitos envolvidos nessa matéria. Vamos lá?
Questões Resolvidas sobre Polias e Roldanas
QUESTÃO 1 – Um garoto constrói um sistema composto por uma roldana, um dinamômetro, um assento e uma corda para facilitar a subida numa árvore. Num primeiro teste, o dinamômetro indica 250 N. O peso real do garoto é 32 kgf e o peso do assento é 16 kgf.
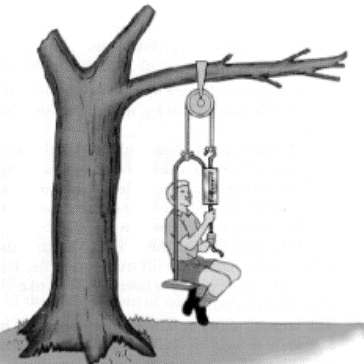
a) Mostre que a aceleração está orientada para cima.
Nesta questão, temos que nos atentar que nos é dado o peso em kgf e nossas contas devem ser feitas em N. Então, precisamos converter. Para isso, devemos lembrar que, na Terra: 1 kgf ≅ 10 N. Portanto, o peso do garoto vale 32 N e do assento, 160 N.
Para mostrar que a aceleração está para cima, temos que lembrar que: FR = m . a. Para que a aceleração esteja para acima, basta que a resultante aponte para cima. Então, vamos considerar tudo (o garoto, o assento, o dinamômetro, a roldana e a corda) como um sistema só.
Neste sistema, atua uma força de tração no fio na mão do garoto (T) que vale 250 N. Este mesmo fio está conectado na balança, ou seja, a tração neste outro fio também vale 250 N (vamos lembrar que, em um fio ideal, a tração nas duas pontas é a mesma).
Para baixo, vamos ter o peso do assento (160 N) e do garoto (320 N). Veja que há mais força para cima do que para baixo. Calculando:
Fcima = 250 + 250
Fcima = 500 N
Fbaixo = 160 + 320
Fbaixo = 480 N
Com isso, temos que a força resultante está para cima, pois para baixo há menos força:
FR = 500 – 480
FR = 20 N
Se a resultante está orientada para cima, a aceleração também está, pois elas sempre têm o mesmo sentido.
b) Determine a intensidade da força que o garoto troca com o assento.
Quando a questão nos pede isso, a melhor saída é isolar o garoto para fazer as contas, pois a força que ele vai trocar com o assento é a normal.
Isolando o garoto, temos a tração agindo para cima com 250 N, atua também uma normal embaixo dele e também há o peso do próprio garoto, que vale 320 N. Além disso, já sabemos que o garoto acelera para cima, ou seja, a força resultante que atua sobre ele também deve estar para cima.
Como a resultante é sempre a força que ajuda menos a força que atrapalha, teremos:
FR = m . a
250 + N – 320 = 32 . a
Temos que calcular a aceleração do conjunto, pois considerando tudo como um único sistema, podemos utilizar a resultante que descobrimos no item A para fazer as contas:
FR = m . a
20 = (32 + 16) . a
a = 20/48 m/s²
Voltando à nossa conta sobre o garoto:
250 + N – 320 = 32 . 20/48
N = 83,3 N
QUESTÃO 2 – (ITA) Dois blocos de mesma massa M estão unidos por um fio de massa desprezível que passa por uma roldana sem atrito com um eixo fixo. Um terceiro bloco de massa m é colocado suavemente sobre um dos blocos, como mostra a figura. A intensidade da força que esse pequeno bloco de massa m pressionará o bloco sobre o qual foi colocado vale:
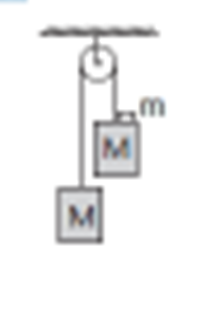
RESOLUÇÃO:
Nesta questão podemos considerar o corpo M que está mais baixa como corpo A e os corpos M e m como corpo B e fazer que:
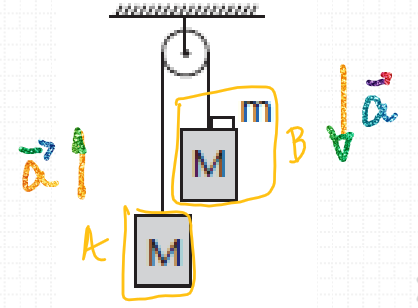
FR = mtotal . a
Nesse caso, a resultante será sempre o peso maior (B) menos o peso menor (A). Ficaremos com:
PB – PA = (mA + mB) . a
Lembrando que P = m . g:
m. g + M . g – M . g = (M + M + m) . a
m . g = (2M + m) . a

Como a questão nos perguntou a força de contato entre M e m, temos que isolar um dos dois. O mais fácil, nesse caso, é usar m, pois sobre M agem mais forças.
Então, isolando m, teremos o peso (P) para baixo e a normal (N) para cima. Perceba que esse corpo acelera para baixo, pois está do lado mais pesado da roldana.
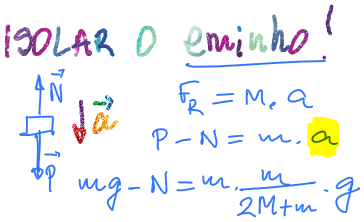
Ai vem a matemática para isolar a normal N
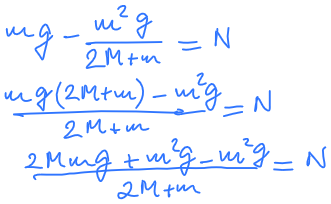
RESPOSTA: A
QUESTÃO 3 – O esquema mostrado na figura abaixo é chamado de Moitão Talha, utilizado para que tenha um “ganho de força” no levantamento do corpo A, de peso P.
a) Qual a vantagem mecânica do sistema?
Vamos lembrar que para calcular a vantagem mecânica podemos utilizar:
VM = 2N, onde N é o número de polias móveis. Porém, temos que tomar cuidado, porque nem sempre essa fórmula é válida. E é o caso desta questão.
Isso posto, veja que, quando a pessoa puxa a corda com a força F, ela não vai sentir todo o peso do sistema. Algo que temos que ter claro nesse exercício é: quando a pessoa puxar a corda, qual é a parte do sistema que vai se mexer?
Veja que as polias de cima são fixas, ou seja, não saem do lugar.Já as polias de baixo são móveis. Então, para fazer as contas, vamos juntar as três polias móveis e o corpo A em um único sistema, pois tudo isso vai ficar em equilíbrio.
Uma vez que está em equilíbrio, devemos pensar no quanto de força atua para cima. No que, enquanto o fio for o mesmo, a tração é a mesma. Então, veja que temos o mesmo desde a mão da pessoa até o teto, passando pelas três polias fixas e pelas três móveis.
Nesse sistema com as três polias móveis e o corpo A teremos o peso de A (PA) para baixo. Perceba que nesse recorte da figura, o fio foi cortado por 6 vezes. Cada vez que isso acontece, temos uma tração (T). E essa tração é a mesma força F da imagem. Ou seja: 6F = PA.
Portanto, todo esse sistema de polias reduz em seis vezes a força do peso que a pessoa está levantando.
Concluindo: a vantagem mecânica da máquina é igual a 6.
b) Se o ponto x descer 15 cm, qual será o deslocamento de A?
Nesta máquina, temos um defeito: ganha-se em força, mas perde-se em deslocamento. Isso porque o trabalho (τ) sem dissipação de energia de um lado é igual ao do outro. E trabalho é calculado pela divisão de força pelo deslocamento, ou seja, são inversamente proporcionais. Então, do lado que temos menos força, há mais deslocamento, e vice-versa.
Portanto, temos:
|τPA| = |τF|
PA . hA = F . Δx
Como sabemos que a força F vale um sexto do peso:
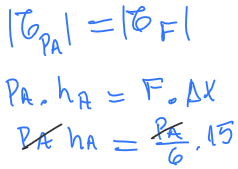
hA = 2,5 cm
Para aprender mais
Assista à resolução desses e de outros exercícios no meu canal:
Espero que você tenha entendido um pouco melhor sobre polias e roldanas. E se quiser ajuda para melhorar seu nível de Física em outras matérias, entre em contato comigo e escolha o curso de Física mais adequado para você!
SAIBA MAIS
🐧 Resumo com exercícios sobre Lançamento horizontal
🐧 Entenda o que é Movimento Vertical no Vácuo
🐧 Lista de exercícios: 1ª Lei Termodinâmica e Transformações
Me acompanhe nas redes sociais: curta a minha página no Facebook, me siga no Instagram, se inscreva no Youtube e participe do meu canal oficial no Telegram.

