Exercícios Resolvidos de Cinemática
1. (G1 – IFSC) Hoje sabemos que a Terra gira ao redor do Sol (sistema heliocêntrico), assim como todos os demais planetas do nosso sistema solar. Mas na Antiguidade, o homem acreditava ser o centro do Universo, tanto que considerava a Terra como centro do sistema planetário (sistema geocêntrico). Tal consideração estava baseada nas observações cotidianas, pois as pessoas observavam o Sol girando em torno da Terra.
É CORRETO afirmar que o homem da Antiguidade concluiu que o Sol girava em torno da Terra devido ao fato que:
a) considerou o Sol como seu sistema de referência.
b) considerou a Terra como seu sistema de referência.
c) esqueceu de adotar um sistema de referência.
d) considerou a Lua como seu sistema de referência.
e) considerou as estrelas como seu sistema de referência.
Resposta: alternativa b) considerou a Terra como seu sistema de referência.
Do ponto de vista do homem da Antiguidade, era o Sol que girava em torno da Terra, e não o contrário, pois, em seu referencial, a Terra estava parada e o Sol estava em movimento.
2. (PUC- PR) Em relação a um avião que voa horizontalmente com velocidade constante, a trajetória das bombas por ele abandonadas é:
a) uma reta inclinada;
b) uma parábola de concavidade para baixo;
c) uma reta vertical;
d) uma parábola de concavidade para cima;
e) um arco de circunferência.
Resposta: alternativa c) uma reta vertical.
Do ponto de vista do avião (referencial), a movimentação da bomba é apenas para baixo, pois ela segue a trajetória horizontal do avião juntamente com seu movimento vertical. Para uma pessoa no chão, no entanto, a trajetória das bombas é uma parábola voltada para baixo.
3. (UERJ) A figura abaixo representa uma escuna atracada ao cais.
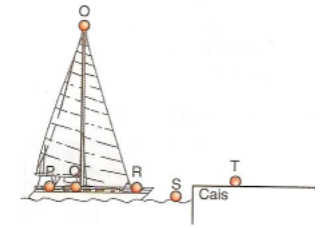
Deixa-se cair uma bola de chumbo do alto do mastro, ponto O. Nesse caso, ela cairá ao pé do mastro, ponto Q. Quando a escuna estiver se afastando do cais, com velocidade constante, se a mesma bola for abandonada do mesmo ponto O, ela cairá no seguinte ponto da figura:
a) P
b) Q
c) R
d) S
e) T
Resposta: alternativa b) Q
Como a bola se movimenta junto com a escuna (ou seja, está parada em relação à escuna), mesmo com o barco em movimento sua trajetória continua sendo uma linha reta para baixo. Então, ela cai exatamente no mesmo ponto.
4. (UFMG-MG) Um estudante, observando seus colegas assentados em seus lugares e recordando seus conceitos de movimento, julga corretamente que:
a) como não há repouso absoluto, nenhum de nós está em repouso em relação a nenhum referencial.
b) a velocidade de todos os estudantes que eu consigo enxergar agora assentados em seus lugares, é nula para qualquer observador.
c) mesmo para o professor, que não pára de andar, seria possível achar um referencial em que ele estivesse em repouso.
d) eu estou em repouso em relação aos meus colegas, mas todos nós estamos em movimento em relação à Terra.
Resposta: alternativa c) mesmo para o professor, que não pára de andar, seria possível achar um referencial em que ele estivesse em repouso.
Para qualquer corpo (referencial) que fizesse a mesma trajetória com o professor, como uma caneta em seu bolso, o professor estaria em repouso.
5. Dois corpos A e B se movem em trajetórias retilíneas, paralelas e muito próximas.
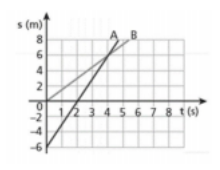
a) Qual a distância inicial entre os corpos?
Resposta: 6m
A distância inicial entre os dois corpos vai ser no instante 0, e que a posição inicial de B é igual a 0 (SAb = 0) e a posição inicial de A é -6 (S0A = -6m). Então a distância inicial é igual a 6m (Dab = 6m).
b) Qual o instante de encontro?
Resposta: 𝚫t = 4s
É o instante em que os gráficos se cruzam. Como o gráfico nos dá a escala, podemos perceber que este instante corresponde a 𝚫t = 4s.
6. Os espaços de um móvel obedecem à função horária s = 150 – 10.t (SI). O instante em que o móvel passa pela origem dos espaços é:
a) – 15 s
b) 15 s
c) 10 s
d) 5 s
e) – 10 s
Resposta: b) 15 s
Passar pela origem dos espaços é passar por onde a trajetória (s) é igual a 0. Então basta substituir o s da equação por 0.
s = 150 – 10t
0 = 150 – 10t
10t = 150
t = 15s
7. Um móvel se locomove sobre uma trajetória retilínea de acordo com o gráfico de posição versus tempo a seguir.

Determine:
a) a variação de espaço entre os instantes t = 0 e t = 6 s.
Resposta: 10m
No instante 0s, o espaço é -10m. No instante 6s, o espaço é 0m. Então basta calcular a diferença 𝚫S, dada pela equação 𝚫S = S – S0.
𝚫S = S – S0
𝚫S = 0 – (-10)
𝚫S = 10m
b) a distância efetivamente percorrida neste intervalo
Resposta: 30m
Perceba que o móvel tem um movimento de ida, fica alguns instantes parado e depois tem um movimento de volta. Então temos que somar o 𝚫S na ida e o 𝚫S na volta.
Dp = 𝚫S(ida) + 𝚫S(volta)
Não se esqueça que deve usar a distância em módulo, e que o 𝚫S = S – S0
Dp = |10 – (-10)| + |0 – 10|
Dp = |20| + |10|
Dp = 30m
c) o deslocamento escalar entre t = 0 e t = 8 s
Resposta: 0m
Deslocamento escalar é 𝚫S, sendo 𝚫S = S – S0. Então vamos fazer essa conta.
𝚫S = S – S0
𝚫S = -10 – (-10)
𝚫S = -10 + 10
𝚫S = 0m
O deslocamento é nulo pois ele voltou para o ponto de partida.
Espero que você tenha entendido um pouco melhor sobre cinemática. E se quiser ajuda para melhorar seu nível de Física em outras matérias, entre em contato comigo e escolha o curso de Física mais adequado para você!

SAIBA MAIS
✅ Conceitos básicos de Cinemática: Repouso e movimento
✅ Questões de Cinemática resolvida em vídeo
✅ Conceitos básicos de Cinemática: Equação do espaço em função do tempo
Me acompanhe nas redes sociais: curta a minha página no Facebook, me siga no Instagram, se inscreva no Youtube e participe do meu canal oficial no Telegram.

