Olá, pessoal, tudo bem?
Nesta aula, vamos fazer uma revisão completa sobre subtração vetorial. Vamos lá?
Grandezas Escalares e Vetoriais
Há algumas grandezas que, para estarem definidas, precisam apenas do número e uma unidade, como massa, temperatura e volume. Essas grandezas são conhecidas como grandezas escalares. Entretanto, há grandezas que, para serem definidas, necessitam de mais dados, como informações geométricas, para entendermos sua direção e sentido.
É o caso, por exemplo, da grandeza força. A unidade de força é o Newton, dada pelo Sistema Internacional. Então, quando dizemos que uma força vale 200 Newtons, precisamos acrescentar a direção e sentido para a qual ela age.
Para que a grandeza força fique definida, usamos uma seta para apontar o lado para o qual ela atua. Essas setas são conhecidas como vetores e as grandezas que necessitam deles, grandezas vetoriais. Entre os exemplos de força vetorial estão a aceleração, a força e a velocidade.
Vetores
Para simbolizar um vetor, utilizamos uma letra com uma pequena seta, como podemos ver na figura abaixo:
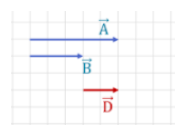
O tamanho do vetor é conhecido como módulo. Para representar o módulo de um vetor A, usamos o símbolo . Quando dois vetores são paralelos ou estão sobre a mesma reta, diz-se que eles possuem a mesma direção.
Na imagem acima, por exemplo, os 3 vetores têm a mesma direção. Já na imagem abaixo, o vetor B tem a mesma direção que os vetores A e D, mas eles apontam para sentidos opostos.
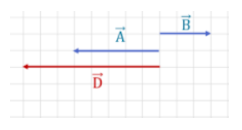
Então, podemos dizer que A e B têm sentidos opostos, enquanto A e D têm o mesmo sentido. Diz-se que 2 vetores são iguais quando possuem o mesmo módulo, a mesma direção e o mesmo sentido. Para concluirmos a introdução aos vetores, admite-se a existência do vetor nulo,, cujo vetor possui módulo igual a zero. Neste caso, sua representação é um ponto.
Subtração de vetores
Para pensar em subtração de vetores, a operação será semelhante à soma de vetores, mas você terá que inverter um deles para realizar a operação diretamente. Vamos dividir essa operação em dois tipos: a subtração de vetores de mesma direção e a subtração de vetores não paralelos.
Subtração de vetores de mesma direção
Para entendermos melhor a operação, vamos começar analisando um exemplo. Temos abaixo a imagem de dois vetores que formam um ângulo de 0º (ou seja, mesma direção). então vamos calcular a diferença (vetor D), que é vetor A – vetor B. Neste caso, é só subtrair um valor de outro, porque os dois têm o mesmo sentido.
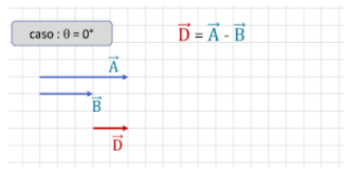
Vamos supor então que o vetor A tenha 5 unidades e o vetor B, 3 unidades. Então, basta subtrair do módulo do A o módulo do B, como ilustrado abaixo, que resulta em 2 unidades:

O resultado é um vetor D com duas unidades, que aponta para a direita.
No caso de vetores de mesma direção mas sentidos diferentes é um pouco mais complicado. Vamos ver o exemplo abaixo:
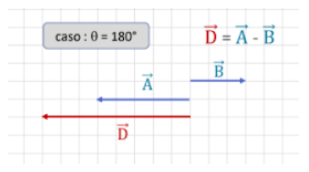
Neste caso, você somará o módulo dos dois vetores, mas colocará um deles (neste caso, o vetor B) com o sinal oposto. Porém, como estamos falando de módulos, a soma se dá apenas nas unidades:
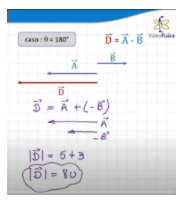
Neste caso, a soma dos 2 vetores é igual a 8 unidades.
Subtração de vetores não paralelos
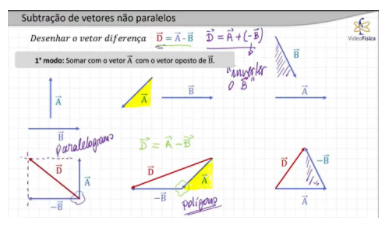
Neste caso, existem duas regras a serem usadas. A primeira regra é somar um dos vetores com o oposto do outro. A partir disso, você pode usar as regras da adição, como a regra do paralelogramo e a regra do polígono. Vamos aos exemplos para relembrarmos como faz:
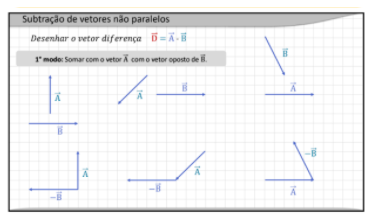
Temos acima 3 exemplos e vamos usar então o primeiro modo. Como eu disse, vamos somar um dos vetores com o oposto do outro – aqui, eu já escolhi qual deles será usado como oposto, mas você pode escolher qualquer um dos dois. No primeiro caso, como coloquei os dois vetores com a mesma origem, vou usar a regra do paralelogramo, traçando um paralelogramo e colocando vetor resultante ali:
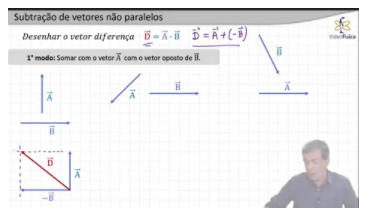
No segundo exemplo, vou usar a regra do polígono. Então, pegue um dos vetores e coloque o segundo vetor com sinal oposto com sua origem no fim do outro vetor. Depois, basta fechar a figura para encontrar o vetor diferença.
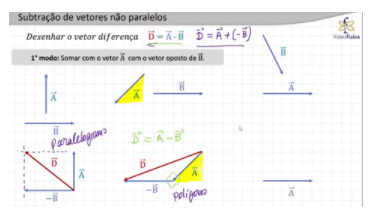
No terceiro exemplo, começamos da mesma forma: invertendo o sentido de um dos vetores; vou usar a mesma técnica que no segundo exemplo, a regra do polígono, ou seja, a origem de um dos vetores fica no fim do outro vetor. Aí, é só traçar um vetor fechando a figura e temos o vetor D.
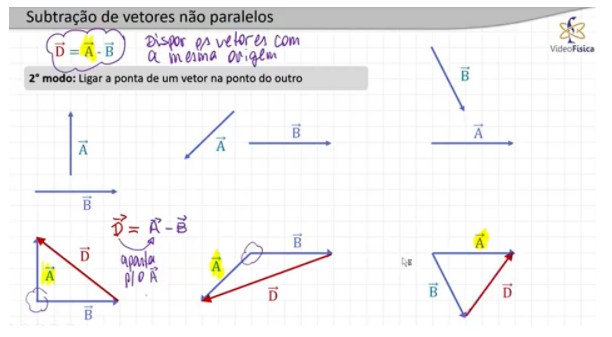
O segundo modo de subtração de vetores não paralelos é simplesmente unir a origem dos dois, sem a necessidade de trocar o sentido de um deles. Neste caso, basta unir a origem dos dois vetores e depois unir a ponta desses dois vetores, dando origem a um vetor diferença.
O vetor diferença sempre apontará para o primeiro vetor escrito na equação. Por exemplo, se o cálculo for vetor A – B, então o vetor diferença apontará para o vetor A. Por isso, é preciso prestar atenção no enunciado, pois ele indicará para onde deve apontar o vetor D.
Lembre-se de que subtração de vetores não é um conteúdo que caia tanto no vestibular; a soma de vetores é um conteúdo mais frequente. Então, estude bastante soma vetorial com ajuda do meu vídeo sobre o assunto.
–
Espero que você tenha entendido um pouco melhor sobre subtração vetorial. E se quiser ajuda para melhorar seu nível de Física em outras matérias, entre em contato comigo e escolha o curso de Física mais adequado para você!
Tem dúvidas de como funciona a minha plataforma e a minha metodologia de ensino? Clique aqui e acesse gratuitamente os módulos de Cinemática e Óptica do meu SEMIEXTENSIVO exclusivo para FUVEST, UNICAMP, UNESP E UNIFESP. Tenho certeza que vai mudar a sua vida.

Me acompanhe nas redes sociais: curta a minha página no Facebook, me siga no Instagram, se inscreva no Youtube e participe do meu canal oficial no Telegram.



