A Termometria é a área da Física que estuda temperatura e as escalas termométricas, como Celsius, Fahrenheit e Kelvin.
Veja como fazer a transformação de uma escala de temperatura para outra
Para você saber as temperaturas em diferentes escalas, é preciso conhecer os pontos fixos nessas escalas. São dois pontos fixos das escalas termométricas:
- O ponto de fusão do gelo, que é quando o gelo derrete;
- O ponto de ebulição da água, que é quando a água evapora.
Na escala Celsius, que é a que mais conhecemos e utilizamos, esses pontos são 0º e 100º, respectivamente. Na escala Kelvin, bastante usada no meio científico, os pontos de fusão do gelo e ebulição da água são respectivamente 273 K e 373 K. Já na escala Fahrenheit, o ponto de fusão do gelo é 32ºF, enquanto o de ebulição da água é 212 ºF. E, não adianta: esses valores nós precisamos memorizar mesmo.
Transformação de Celsius para Kelvin (e vice-versa)
Uma vantagem é que o intervalo de temperatura é igual entre os ponto de fusão do gelo e de ebulição da água tanto em Celsius quanto em Kelvin, ou seja, 100 graus separam o ponto de fusão e de ebulição nos dois sistemas. Já no sistema Fahrenheit temos 180 graus.

Para poder transformar a medida de uma escala na outra, é preciso fazer proporção entre os segmentos. Por exemplo, vamos criar uma fórmula que converta uma temperatura da escala Celsius para a escala Kelvin.
Eu já sei que 0 ºC corresponde a 273 K, e que 100 ºC corresponde a 373 K. Então, se eu tiver um número qualquer (ϴ) em Celsius, quanto será esse número em Kelvin?
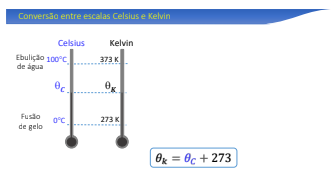
Essa correspondência é colocada pela fórmula ϴk = ϴc + 273
Ou seja: se você tiver a temperatura em Kelvin, basta substituí-la por ϴk para achar a temperatura em Celsius, e vice-versa.
Por exemplo, se tenho uma temperatura em Celsius de 27 ºC, colocando na fórmula, temos:
ϴk = 27 + 273
ϴk = 300 K
Se você não quiser usar a fórmula, basta criar uma equação de equivalência:
ϴc – 0 ϴk – 273
——— = ———–
100 – 0 373 – 273
ϴc ϴk – 273
—— = ———–
100 100
ϴc = ϴk – 273
ou
ϴk = ϴc + 273
Ou seja, chegamos à fórmula dada, mas fazendo todos os passos da equação de equivalência.
Zero absoluto
Zero absoluto é a menor temperatura fisicamente possível, na qual o nível de agitação das partículas é nulo. Em tese, neste caso todas as partículas estariam sem agitação. O zero absoluto está na escala Kelvin. Ou seja, para encontrá-lo em Celsius, basta jogar na fórmula:
ϴk = ϴc + 273
0 = ϴc + 273
ϴc = -273 ºC
Transformação de Celsius para Fahrenheit (e vice-versa)
No caso da transformação de Celsius para Fahrenheit (e vice-versa), não temos o mesmo intervalo de temperatura, pois os 100 ºC correspondem a 180 ºF. Assim, neste caso a fórmula é um pouco mais complexa.
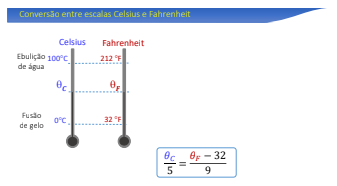
Mas nem sempre é preciso decorar as fórmulas, basta você criar uma relação de proporção entre as duas escalas.
Por exemplo:
ϴc – 0 ϴf – 32
——— = ———–
100 – 0 212 – 32
Simplificando, temos:
ϴc ϴf – 32
—— = ———–
100 180
ϴc ϴf – 32
—— = ———–
5 9
Novamente, chegamos na mesma fórmula, e da mesma maneira podemos montar relações entre diferentes escalas termométricas. Basta saber os valores de fusão do gelo e ebulição da água de cada escala.
Exercícios de Termometria
Agora vamos resolver alguns exercícios para ver se você entendeu bem.
1. A temperatura normal de funcionamento do motor de um automóvel é 90°C. Determine essa temperatura em graus Fahrenheit e em Kelvin.
Bom, quem quiser fazer pela fórmula, é só substituir:
ϴc ϴf – 32
—— = ———–
5 9
90 ϴf – 32
—— = ———–
5 9
ϴf – 32
18 = ———–
9
18 x 9 = ϴf – 32
162 = ϴf – 32
ϴf = 162 + 32
ϴf = 194 ºF
ϴk = ϴc + 273
ϴk = 90 + 273
ϴk = 363 K
Se você não quiser usar as fórmulas prontas, basta fazer os termômetros um ao lado do outro e fazer aquela equação de relação que vimos anteriormente.
2. A indicação de uma temperatura na escala Fahrenheit excede em duas unidades o dobro da correspondente indicação na escala Celsius. Essa temperatura é:
a) 300 °C b) 150 ° C c) 50 ° C d) 170 ° C e) 100 ° C
Para começarmos, precisamos transformar o enunciado em um fórmula:
F = 2C + 2
Agora, basta colocar isso na fórmula:
C F – 32
—— = ———–
5 9
C 2C + 2 – 32
—— = ——————-
5 9
C 2C – 30
—— = ————
5 9
9C = (2C – 30) x 5
9C = 10C – 150
9C = 10C – 150
150 = 10C – 9C
C = 150 °C
Ou seja, a alternativa certa é b) 150 ° C.
Quer saber mais sobre o assunto? Confira uma videoaula abaixo
E se você tiver dúvidas sobre esse conteúdo, vou te fazer um convite: Que tal fazer parte do meu extensivo 2022 com 20% OFF? Lá, o pessoal já está estudando sobre Vetores, mas com muitas vantagens, como:
🔹 Estudo dirigido da teoria com slides e material de apoio pra você baixar e até imprimir se quiser;
🔹 Lista de Exercícios separados por dificuldade: Básico, Intermediário e Avançado;
🔹 Monitoria individual pra você tirar suas dúvidas sobre o assunto, caso tenha dúvidas no exercícios por exemplo;
🔹 Telegram de estudos exclusivo comigo e com outros alunos como você;
🔹 Encontros ao vivo em grupo pra batermos um papo sobre física.

Demais não é? Aperte aqui e use o cupom BLOG20 para se inscrever com 20% OFF e iniciar ainda hoje seus estudos na melhor plataforma de física do país.
SAIBA MAIS
👉 Exercícios de Termometria
👉 Como estudar Termologia para vestibulares paulista
👉 Questões de Termologia, óptica, eletrodinâmica e ondulatória
Me acompanhe nas redes sociais: curta a minha página no Facebook, me siga no Instagram, se inscreva no Youtube e participe do meu canal oficial no Telegram.

