Olá, pessoal, tudo bem? Neste post, vamos falar sobre gás ideal: suas características, lei geral e um exercícios resolvido para treinar. Vamos lá?
Gás ideal: o que é?
O gás ideal ou gás perfeito é um modelo teórico em que muitas partículas diminutas se movem de maneira aleatória com diferentes velocidades, sofrendo somente colisões perfeitamente elásticas entre si.
O conceito de gás ideal é essencial para o estudo dos gases, já que muitos dos gases reais se comportam como gases ideais quando submetidos a baixas pressões e altas temperaturas. Também auxilia na compreensão das transformações gasosas, da lei geral dos gases, equação de Clapeyron etc.
Gás ideal: variáveis de estado de um gás natural
As variáveis de estado de um gás natural são 3:
- Pressão do gás (p): depende das colisões das partículas contra o recipiente. Para calculá-la usamos a fórmula p = F/A (sendo F = força e A = área). No sistema Internacional (SI), a pressão é medida em Newton/m², que nada mais é do que a unidade pascal (Pa). Se quiser saber em ATM, basta fazer a conversão com a seguinte fórmula 1 ATM = 10⁵Pa
- Volume do gás (V): tanto volume quanto forma dependem do recipiente. No Sistema Internacional, usamos o metro cúbico (m³) para mensurar o volume, mas usa-se muito o litro (L), então basta fazer a conversão: 1 L = 10⁻³ m³, ou 1 cm³ = 10⁻⁶ m³
- Temperatura do gás (T): é importante ficar ligado de que, nesta matéria, a temperatura é sempre calculada em Kelvin (K). Ela está relacionada à agitação térmica das moléculas.
Gás ideal: equação de estado do gás
A equação de estado do gás ou equação de Clapeyron é uma das mais importantes para o estudo do gás ideal, e é dada por p.V = n.R.T, onde n é a massa de mol do gás. O mol é calculado por n = m/M, onde m é a massa e M é a massa molar (lembre-se das aulas de Química). Já R é a constante universal dos gases, que é R = 0,082 atm.L/mol.K, quando usar ATM, ou R = 8,31 J/mol.K, quando usar Joule, que nada mais é do que J = N.m. Este último é mais usado pelo SI.
Como n e R são constantes, sabemos que, quanto maior a temperatura, maior é o produto da pressão e do volume, e quanto menor a temperatura, menor o produto da p.V.
Gás ideal: transformações gasosas
Quando houver transformações gasosas, ou seja, um gás passar de um estado 1 para um estado 2, existem várias maneiras de calcular as variáveis usando Clapeyron. Uma delas é isolar aquilo que fica constante nos dois estados, como o R.
Por exemplo:
R = p₁.V₁ / n₁.T₁
R = p₂.V₂ / n₂.T₂
Assim, você pode igualar as duas equações:
p₁.V₁ / n₁.T₁ = p₂.V₂ / n₂.T₂
Outra forma de fazer é relacionar os dois lados:
p₁.V₁ / p₂.V₂ = n₁.T₁ / n₂.T₂
Essa fórmula é muito útil quando o número de mols (n) é diferente nos dois estados (n₁ ≠ n₂).
Ou ainda, usar a Lei geral dos gases, dada por:
p₁.V₁ / T₁ = p₂.V₂ / T₂
Contudo, fique atento, a fórmula acima só vale se o número de mols (n) for constante.
Gás ideal: transformação isobárica
Transformação isobárica é quando a pressão se mantém constante entre o estado 1 e o estado 2 (ou mais estados) de um gás. Se a pressão fica uma constante, então, na equação de Clapeyron, apenas volume e temperatura mudam.
Neste caso, volume e temperatura serão diretamente proporcionais. Isolando o volume na fórmula, eu tenho V = n.R.T / p. Como n.R/p formam uma constante, eu posso classificá-los como a constante K, e a fórmula fica V = K.T. Veja como ficam os gráficos:

Gás ideal: transformação isovolumétrica
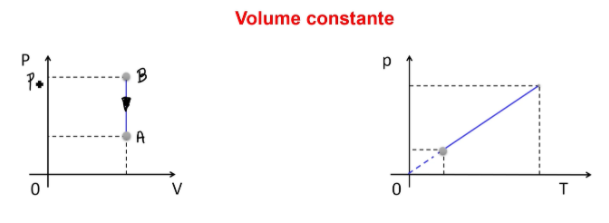
Transformação isovolumétrica, isométrica ou isocórica é quando o volume se mantém constante entre o estado 1 e o estado 2 (ou mais estados) de um gás. Se o volume fica uma constante, então, na equação de Clapeyron, apenas pressão e temperatura mudam.
Neste caso, pressão e temperatura serão diretamente proporcionais. Isolando a pressão na fórmula, eu tenho p = n.R.T / V. Como n.R/V formam uma constante, eu posso classificá-los como a constante K, e a fórmula fica p = K.T. Veja como ficam os gráficos:
Gás ideal: transformação isotérmica
Transformação isotérmica é quando a temperatura se mantém constante entre o estado 1 e o estado 2 (ou mais estados) de um gás. Se a temperatura fica uma constante, então, na equação de Clapeyron, apenas pressão e volume mudam.
Neste caso, pressão e volume serão inversamente proporcionais. Isolando a pressão na fórmula, eu tenho p = n.R.T / V. Como n.R.T formam uma constante, eu posso classificá-los como a constante K, e a fórmula fica p = K/V. Além disso, p₁.V₁ = p₂.V₂. Veja como fica o gráfico:

Caso haja mais de uma curva (que representa a temperatura), quanto mais elevada ela for, maior será a temperatura.
Exercício sobre Gás ideal

(Mackenzie) A figura acima representa duas isotérmicas em que certa massa gasosa, inicialmente no estado A, sofre uma transformação atingindo o estado B, que por sua vez sofre uma transformação, atingindo o estado C. A temperatura T(a) e o volume V(a) são iguais a
a) 200 K e 5 L
b) 300 K e 2 L
c) 400 K e 4 L
d) 500 K e 2 L
e) 500 K e 4 L
Resposta: alternativa d) 500 K e 2 L
Primeiramente, já sabemos que T(a) e T(b) são iguais. Assim, podemos usar
P(b).V(b) / T(b) = P(c).V(c) / T(c)
P(b0 e P(c) são iguais, então:
P(b).V(b) / T(b) = P(c).V(c) / T(c)
5 / T(b) = 3 / 300
T(b) = 500 K
Agora, vamos encontrar o volume:
P(b).V(b) = P(a).V(a)
4 . 5 = 10 . V(a)
V(a) = 2 L
Para aprender mais:
Espero que você tenha entendido um pouco melhor sobre gás ideal. E se quiser ajuda para melhorar seu nível de Física em outras matérias, entre em contato comigo e escolha o curso de Física mais adequado para você!

SAIBA MAIS
🐧 Exercícios sobre Dilatação Térmica Sólidos
🐧 Calorimetria e dilatação térmica
🐧 Exercícios sobre Dilatação de líquidos
Me acompanhe nas redes sociais: curta a minha página no Facebook, me siga no Instagram, se inscreva no Youtube e participe do meu canal oficial no Telegram.

