Oi, pessoal! Belezinha?
Vamos juntos resolver a prova da Santa Casa 2018? As questões estão abaixo e as resoluções, no vídeo. Bora?
Questão 1:
Um motorista dirigia seu automóvel por uma estrada reta. Ao passar pela placa 1, com velocidade de 25 m/s, iniciou a frenagem de seu veículo mantendo uma desaceleração constante até passar pela lombada. Em seu trajeto, passou pela placa 2, com velocidade de 15 m/s.
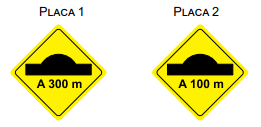
O intervalo de tempo decorrido entre a passagem do veículo pela placa 1 e a passagem pela lombada foi de
(A) 30 s.
(B) 20 s.
(C) 25 s.
(D) 10 s.
(E) 15 s.
Questão 2:
Duas caixas, A e B, estão apoiadas, em repouso, sobre uma superfície plana e horizontal. Sobre a caixa A é aplicada uma força F, horizontal e de intensidade constante, conforme a figura.
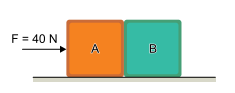
O gráfico representa a variação da intensidade da força Fab, transmitida de A para B, em função da massa de A, mA, mantendo a massa de B, mB, constante.

Desprezando o atrito e a resistência do ar, a aceleração do sistema quando mA = 2 kg será

Questão 3:
A figura representa a trajetória elíptica de determinado planeta em torno do Sol.
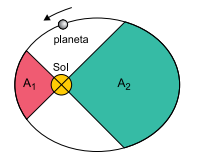
Considerando as proporções entre as áreas indicadas na figura, que a linha imaginária que liga esse planeta ao Sol varre a área A1 em um intervalo de tempo t1 e a área A2 em um intervalo de tempo t2 e sendo válida a Lei das Áreas, de Kepler, é correto afirmar que

Questão 4:
Duas esferas idênticas, A e B, sofrem uma colisão totalmente inelástica. Imediatamente antes da colisão, elas se movem no plano xy, representado na figura, com velocidades vA = 2v e vB = v.

Sabendo que imediatamente depois da colisão elas se movem juntas com velocidade de módulo v’, é correto afirmar que

Questão 5:
Um pêndulo é constituído de uma pequena esfera de massa m presa por meio de um fio ideal de comprimento L a um ponto fixo O. A esfera é abandonada do repouso do ponto A, com o fio inclinado de um ângulo α com a vertical. Depois de passar algumas vezes pelo ponto C, a esfera para instantaneamente no ponto B, com o fio inclinado de um ângulo β com a vertical.

Considerando sen a = 0,9, cos a = 0,4, sen b = 0,6 e cos b = 0,8, a energia mecânica dissipada, desde o início das oscilações até a parada instantânea no ponto B, foi igual a
(A) 0,8·m·g·L
(B) 0,4·m·g·L
(C) 0,2·m·g·L
(D) 0,5·m·g·L
(E) 0,6·m·g·L
Questão 6:
O gráfico representa parte da curva de aquecimento de determinada massa de gelo, inicialmente a uma temperatura de –40 ºC, até transformar-se em água líquida a 20 ºC. As etapas 1, 2 e 3 indicadas ocorrem em intervalos de tempo ∆t1, ∆t2 e ∆t3, respectivamente.

Considerando que a energia necessária para provocar essa transformação tenha sido fornecida por uma fonte térmica de potência constante, que todo o calor fornecido por essa fonte tenha sido absorvido pela massa que sofreu a transformação, que o calor específico do gelo é 0,5 cal/(g·ºC), que o calor
específico da água líquida é 1 cal/(g·ºC) e que o calor latente de fusão do gelo é 80 cal/g, é correto afirmar que

Questão 7:
Dois meios homogêneos e transparentes, A e B, são justapostos e separados pela superfície plana S. Um raio de luz monocromático propaga-se pelo meio A com velocidade 1,5 × 10 elevado a 8 m/s, incide perpendicularmente à superfície de separação entre os meios e passa a propagar-se pelo meio B, com velocidade de raiz quadrada de 6/2 × 10 elevado a 8 m/s , conforme a figura 1.
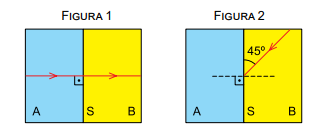
Se esse mesmo raio, propagando-se pelo meio B, incidisse na superfície S conforme a figura 2, ele
(A) refrataria de forma rasante à superfície S.
(B) refrataria fazendo um ângulo de 60º com a superfície
(C) refrataria fazendo um ângulo de 30º com a superfície S.
(D) refrataria fazendo um ângulo de 45º com a superfície S.
(E) sofreria reflexão total
Questão 8:
No mar, quando a amplitude das ondas aumenta, elas perdem seu formato senoidal, suas cristas tornam-se pontudas e seus vales adquirem forma de calha. Quando a amplitude cresce muito, as ondas quebram. Avalia-se, empiricamente, que a onda se quebra quando sua altura (h) atinge 1/7 do comprimento de onda (λ).
(Alberto Gaspar. Física, 2000. Adaptado.)
A velocidade de propagação de uma onda no mar pode, com boa aproximação, ser calculada pela expressão v = raiz quadrada de g . d, em que g é a aceleração da gravidade e d é a profundidade do mar no local da propagação.
Considere que, em uma região onde a profundidade do mar é de 4,9 m, as ondas se quebrem quando sua altura atinge 2 m, conforme a figura.
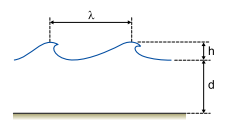
Adotando g = 10 m/s2, a frequência com que as ondas estão oscilando, nessa região, é de
(A) 0,5 Hz.
(B) 2,0 Hz.
(C) 1,5 Hz.
(D) 2,5 Hz.
(E) 1,0 Hz.
Questão 9:
A figura representa um trecho de uma instalação residencial onde estão ligados um ferro de passar e uma lavadora de roupas. A resistência elétrica do ferro é RF = 12 Ω e a lavadora tem força contraeletromotriz E’ = 100 V e resistência interna r’ = 4 Ω.

Para proteger esse trecho do circuito será instalado, na posição indicada na figura, um fusível F escolhido dentre cinco opções diferentes, F1, F2, F3, F4 e F5, que suportam, respectivamente, correntes elétricas máximas de 5, 10, 20, 30 e 40 ampères. Para que esses dois aparelhos elétricos possam funcionar simultaneamente, pode-se instalar

Questão 10:
Uma espira metálica quadrada de lado L move-se com velocidade constante v e atravessa uma região de comprimento 3L onde atua um campo magnético constante B, perpendicular ao plano da figura e com sentido para dentro dela.

Considerando o sentido positivo para a corrente e o eixo x indicados na figura, o gráfico que representa a intensidade da corrente elétrica induzida na espira em função da posição (x) de seu lado vermelho é o indicado em

Tem dúvidas de como funciona a minha plataforma e a minha metodologia de ensino? Clique aqui e acesse gratuitamente os módulos de Cinemática e Óptica do meu SEMIEXTENSIVO exclusivo para FUVEST, UNICAMP, UNESP E UNIFESP. Tenho certeza que vai mudar a sua vida.

Me acompanhe nas redes sociais: curta a minha página no Facebook, me siga no Instagram, se inscreva no Youtube e participe do meu canal oficial no Telegram.


