Olá, pessoal, tudo bem?
Neste post vamos falar um pouco mais sobre Mecânica, mais especificamente trabalho e energia. Vamos dar uma revisada na teoria e nas fórmulas que temos que utilizar para calculá-los e, no final, vamos resolver alguns exercícios, tudo bem?
Lápis e caderno na mão, e vamos juntos!
Como calcular Trabalho e Energia
Existem três maneiras com que podemos fazer nossos cálculos nesta disciplina. Acompanhe:
Quando a força é constante, nós podemos calcular o trabalho da resultante por meio da fórmula:
- τ = FR . d . cosθ
- τ: trabalho, medido em joules (J).
- FR: força resultante, medida em newtons (N).
- d: deslocamento, medido em metros (m).
- cosθ: cosseno do ângulo verificado.
Importante: em Física, o ângulo buscado é, geralmente, aquele formado entre os vetores do mesmo lado da equação. No caso da fórmula acima, entre a força e o deslocamento. Outra forma com que o trabalho da resultante pode ser calculado e que pode ser cobrada nas provas acontece quando não sabemos o seu valor, mas conhecemos o trabalho de cada uma das forças que atuam no corpo.
Quando falamos que o trabalho da resultante pode ser calculado pela fórmula acima, nós temos que saber qual é a resultante que atua no corpo. Mas, e se não soubermos qual é? Nesse caso, temos simplesmente que o trabalho da resultante é igual à soma de todos os trabalhos das forças que atuam sobre o corpo:
- τR = τF1 + τF2 + τF3…
E há ainda uma terceira maneira para calcularmos o trabalho da resultante nos casos em que ela é variável. Como exemplo, temos questões que podem informar o valor da resultante em um gráfico que indique seu valor (em newtons) em função do deslocamento (em metros).
Nesse caso, as variações da força resultante no gráfico vão formar a imagem de um polígono e, assim, basta calcular a área desta figura – geralmente, em um determinado intervalo pedido no enunciado. Veja o exemplo:
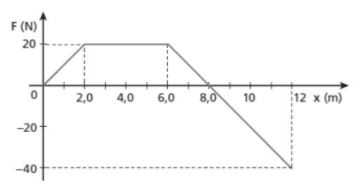
Assim, nesse caso, temos que:
- τR = área do gráfico
Importante: repare em nosso exemplo que, em determinado trecho do gráfico, parte da resultante é negativa. Nessas situações, é necessário dividi-la em outro polígono e calcular sua área. E atenção: esse valor será negativo!
Exercício resolvido
(Colégio Naval/RJ) Observe a figura abaixo
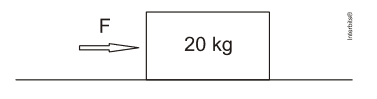
Uma força constante F de 200 N atua sobre o corpo, mostrado na figura acima, deslocando-o por 10 s sobre uma superfície, cujo coeficiente de atrito vale 0,2.
Supondo que, inicialmente, o corpo encontrava-se em repouso, e considerando a gravidade local como sendo 10 m/s² , pode-se afirmar que o trabalho da força resultante, que atuou sobre o bloco, em joules, foi igual a:
a) 20000
b) 32000
c) 40000
d) 64000
e) 80000
RESOLUÇÃO
Como já temos o valor da força F, que atua para a direita com 200 N, vamos começar calculando qual é a força de atrito que tenta impedir o deslocamento do corpo.
Para isso, precisamos usar a seguinte fórmula:
- Fat = µ . N
- Fat: força de atrito
- µ: coeficiente de atrito
- N: força normal
O enunciado já nos forneceu o coeficiente de atrito, que vale 0,2. Já a força normal será igual o peso do corpo. Para calculá-lo, precisamos de outra fórmula:
- P = m . g
- P: peso
- m: massa
- g: gravidade
Portanto, P = 200N.
Voltando à nossa fórmula da força de atrito, temos:
- Fat = µ . N
- Fat = 0,2 . 200
- Fat = 40 N.
Com esses dados em mãos, vamos adiante para calcular a força resultante. Nós sabemos que:
- FR = F – Fat
- FR = 200 – 40
- FR = 160 N
Agora, lembremos da fórmula do trabalho da resultante:
- τR = FR . d . cosθ
Repare que não apenas já conhecemos a força resultante, como também o cosseno do ângulo. Como a resultante está a favor do deslocamento, o ângulo aqui será de 0º, cujo cosseno é 1.
Para aplicarmos a fórmula, falta-nos, portanto, conhecer o deslocamento. Para determiná-lo, devemos ter em mente que, neste caso, trata-se de um MUV (movimento uniformemente variado). Assim, podemos utilizar a fórmula:
- Δs = V0 . t + (a . t²) ÷ 2
No entanto, veja que precisamos conhecer a aceleração. Para isso, nosso primeiro passo vai ser utilizar a 2ª Lei de Newton:
- FR = m . a
- 160 = 20 . a
- a = 8 m/s²
Agora sim: vamos calcular o MUV:
- Δs = V0 . t + (a . t²) ÷ 2
- d = 0 + (8 . 10²) ÷ 2
- d = 400 m
Assim, teremos:
τR = FR . d . cosθ
τR = 160 . 400 . 1
τR = 64000 J
RESPOSTA: D
Espero que você tenha entendido um pouco melhor sobre a teoria e os cálculos sobre Trabalho e Energia. E se quiser ajuda para melhorar seu nível de Física em outras matérias, entre em contato comigo e escolha o curso de Física mais adequado para você!

Tem dúvidas de como funciona a minha plataforma e a minha metodologia de ensino? Clique aqui e acesse gratuitamente os módulos de Cinemática e Óptica do meu SEMIEXTENSIVO exclusivo para FUVEST, UNICAMP, UNESP E UNIFESP. Tenho certeza que vai mudar a sua vida.

Me acompanhe nas redes sociais: curta a minha página no Facebook, me siga no Instagram, se inscreva no Youtube e participe do meu canal oficial no Telegram.
