Fala, pessoal, tudo bem?
Neste post, vamos nos aprofundar um pouco mais em um conteúdo bem interessante da Física: a estática do ponto material. Vamos dar uma relembrada na teoria e, no final, resolveremos um exercícios juntos, ok?
Então, caderno aberto, atenção constante e vamos lá!
Estática de um ponto material: o que é e como calcular?
A Estática é uma área da Mecânica que estuda o equilíbrio dos corpos. Dentro dela, está o nosso foco de hoje: a estática do ponto material. Um corpo – ou ponto material – está sujeito à ação de uma série de forças, em diferentes sentidos.
Pois bem, o conceito de estática do ponto material nos diz que um corpo está em equilíbrio se a resultante das forças que agem sobre ele é nula. Ou seja, a soma vetorial das forças deve ser igual a zero.
Bom, pessoal, isto posto, existem duas formas como podemos calcular a estática de um ponto material: decomposição vetorial ou método da linha poligonal. Vamos conhecer as duas formas:
Imagine que sobre um corpo atuam três forças distintas:
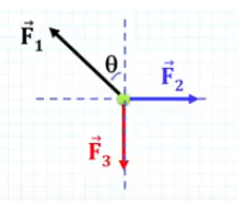
Agora, imagine que a questão forneça o valor de F3 e o ângulo θ formado por F1, e peça para calcular o módulo de F1. Como resolver?
Vamos ver o método por decomposição vetorial:
O primeiro passo é decompor a força F1, que está inclinada, em F1x, que corresponde ao eixo horizontal, e F1y, que corresponde ao eixo vertical.
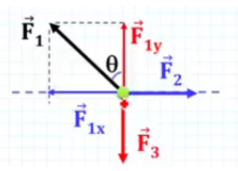
Vimos que, para que esteja em equilíbrio, a força resultante deve ser nula, isto é, a soma dos módulos das forças para cima deve ser igual às para baixo, e que a soma dos módulos das forças para a direita deve ser igual às para esquerda:
- ΣFbaixo = ΣFcima
- ΣFesquerda = ΣFdireita
Então, no nosso exemplo, teríamos o seguinte:
- Na vertical: F3 = F1y
- Na horizontal: F1x = F2
Veja que o F1y é adjacente ao ângulo θ; portanto, a melhor fora é calcular o cosseno deste ângulo. Ou seja:
- cosθ = F1y ÷ F1
- F1y = F1 . cosθ
Se uma das componentes é cosseno, então a outra é seno. Veja:
- F1x = F1 . senθ
Agora vamos ver como poderíamos resolver o mesmo problema com o método da linha poligonal ou método dos triângulos. Acompanhe:
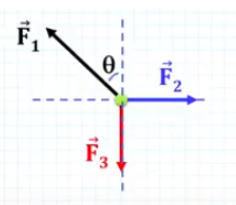
Quando a força resultante é igual a zero, isso significa que nós podemos montar um polígono com as forças. Assim, quando houver três forças atuando sobre o corpo, nós podemos formar um triângulo – que, geralmente, vai ser um triângulo retângulo, ou seja, com um ângulo de 90º.
Bom, para resolver as questões de estática do ponto material por meio de triângulos, é preciso colocar a ponta de cada vetor na origem do outro. Veja:
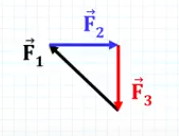
Nesse caso, repare que o ângulo formado entre F1 e F3 será o mesmo ângulo θ fornecido no enunciado. Assim, você já tem dois ângulos em mãos: θ e 90º. A partir daí, é correr para o abraço e fazer os cálculos necessários (seno, cosseno, tangente, Pitágoras etc.).
Exercício resolvido sobre estática do ponto material
(Unesp) Em uma operação de resgate, um helicóptero sobrevoa horizontalmente uma região levando pendurado um recipiente de 200 kg com mantimentos e materiais de primeiros socorros. O recipiente é transportado em movimento retilíneo e uniforme, sujeito às forças peso (P), de resistência do ar horizontal (F) e tração (T), exercida pelo cabo inextensível que o prende ao helicóptero
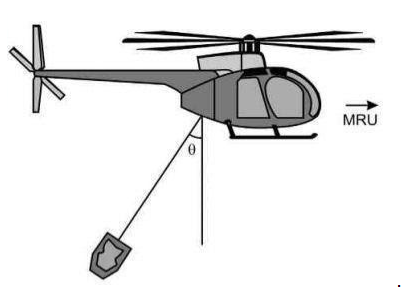
Sabendo que o ângulo entre o cabo e a vertical vale θ, que senθ = 0,6, cosθ = 0,8 e g = 10 m/s², a intensidade da força de resistência do ar que atua sobre o recipiente vale, em N,
a) 500.
b) 1250.
c) 1500.
d) 1750.
e) 3000
RESOLUÇÃO
A primeira coisa que devemos fazer nesta questão é desenhar as forças que agem sobre o recipiente levado pelo helicóptero, para saber se é melhor utilizar a decomposição de vetores ou método dos triângulos.
Ao fazer isso, vemos que, como há três forças que atuam e a força resultante é nula, a melhor maneira é montar um triângulo, sempre lembrando de ligar a ponta dos vetores à extremidade do seguinte:
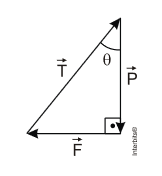
Veja que temos um triângulo retângulo na imagem e que o que queremos descobrir é a força F. Agora repare que já sabemos o valor de P, pois:
P = m . g
P = 200 . 10
P = 2000 N
Assim, se queremos descobrir o cateto oposto (F) e já temos o cateto adjacente (P), basta calcularmos a tangente, ou seja:
tθ = F ÷ P
Lembre-se de que a tangente é calculada com: senθ ÷ cosθ, dados que nos foram fornecidos no enunciado. Assim:
tθ = F ÷ P
senθ ÷ cosθ = F ÷ P
0,6 ÷ 0,8 = F ÷ 2000
F = 1500 N
RESPOSTA: C
Você pode conferir a resolução deste exercício e de muitos outros na minha live especial sobre o assunto. Não perca: Estática Ponto Material.
Espero que você tenha entendido um pouco melhor sobre a teoria e os cálculos sobre estática de um ponto material. E se quiser ajuda para melhorar seu nível de Física em outras matérias, entre em contato comigo e escolha o curso de Física mais adequado para você!
Tem dúvidas de como funciona a minha plataforma e a minha metodologia de ensino? Clique aqui e acesse gratuitamente os módulos de Cinemática e Óptica do meu SEMIEXTENSIVO exclusivo para FUVEST, UNICAMP, UNESP E UNIFESP. Tenho certeza que vai mudar a sua vida.

Me acompanhe nas redes sociais: curta a minha página no Facebook, me siga no Instagram, se inscreva no Youtube e participe do meu canal oficial no Telegram.
